Compute cross-validate eigenvalues

Estimate graph dimension via eigenvalue cross-validation (EigCV). A graph has dimension k if the first k eigenvectors of its adjacency matrix are correlated with its population eigenspace, and the others are not. Edge bootstrapping sub-samples the edges of the graph (without replacement). Edge splitting separates the edges into a training part and a testing part.

Usage

eigcv(
  A,
  k_max,
  ...,
  num_bootstraps = 10,
  test_portion = 0.1,
  alpha = 0.05,
  method = c("none", "holm", "hochberg", "hommel", "bonferroni", "BH", "BY", "fdr"),
  laplacian = FALSE,
  regularize = TRUE
)

Arguments

A: The adjacency matrix of graph. Must be non-negative and integer valued.
k_max: The maximum dimension of the graph to consider. This many eigenvectors are computed. Should be a non-negative integer smallish relative the dimensions of A.
...: Ignored.
num_bootstraps: The number of times to bootstrap the graph. Since cross-validated eigenvalues are based on a random graph split, they are themselves random. By repeatedly computing cross-validated eigenvalues for different sample splits, the idea is to smooth away some of the randomness due to the graph splits. A small number of bootstraps (3 to 10) usually suffices. Defaults to 10. Test statistics (i.e. z-scores for cv eigenvalues) are averaged across bootstraps and the p-values will be calculated based on the averaged statistics.
test_portion: The portion of the graph to put into the test graph, as opposed to the training graph. Defaults to 0.1. Must be strictly between zero and one.
alpha: Significance level for hypothesis tests. Each dimension 1, ..., k_max is tested when estimating graph dimension, and the overall graph dimension is taken to be the smallest number of dimensions such that all the tests reject.
method: Method to adjust p-values for multiple testing. Must be one of "none", "holm", "hochberg", "hommel", "bonferroni", "BH", "BY", or "fdr". Passed to stats::p.adjust(). Defaults to "none".
laplacian: Logical value indicating where to compute cross-validated eigenvalues for the degree-normalize graph Laplacian rather than the graph adjacency matrix. Experimental and should be used with caution. Defaults to FALSE.
regularize: Only applicable when laplacian == TRUE, in which case this parameter controls whether or not the degree-normalized graph Laplacian is regularized. Defaults to TRUE.

Value

A eigcv object, which is a list with the following named elements.

estimated_dimension: inferred graph dimension.
summary: summary table of the tests.
num_bootstraps: number of bootstraps performed.
test_portion: graph splitting probability used.
alpha: significance level of each test.

Examples


library(fastRG)

set.seed(27)

B <- matrix(0.1, 5, 5)
diag(B) <- 0.3

model <- sbm(
  n = 1000,
  k = 5,
  B = B,
  expected_degree = 40,
  poisson_edges = FALSE,
  allow_self_loops = FALSE
)

A <- sample_sparse(model)

eigs<- eigcv(A, k_max = 10)
#> 'as(<dsCMatrix>, "dgCMatrix")' is deprecated.
#> Use 'as(., "generalMatrix")' instead.
#> See help("Deprecated") and help("Matrix-deprecated").
eigs
#> Estimated graph dimension:	 5
#> 
#> Number of bootstraps:		 10
#> Edge splitting probabaility:	 0.1
#> Significance level:		 0.05
#> 
#>  ------------ Summary of Tests ------------
#>   k          z        pvals         padj
#>   1 60.0858888 0.000000e+00 0.000000e+00
#>   2 11.7538714 3.372802e-32 3.372802e-32
#>   3 11.1552401 3.375515e-29 3.375515e-29
#>   4 11.3242906 4.974047e-30 4.974047e-30
#>   5  9.5379830 7.281856e-22 7.281856e-22
#>   6 -1.1633387 8.776540e-01 8.776540e-01
#>   7 -1.2996582 9.031409e-01 9.031409e-01
#>   8 -1.1750915 8.800209e-01 8.800209e-01
#>   9 -1.1354378 8.719040e-01 8.719040e-01
#>  10 -0.8694766 8.077067e-01 8.077067e-01
#> 

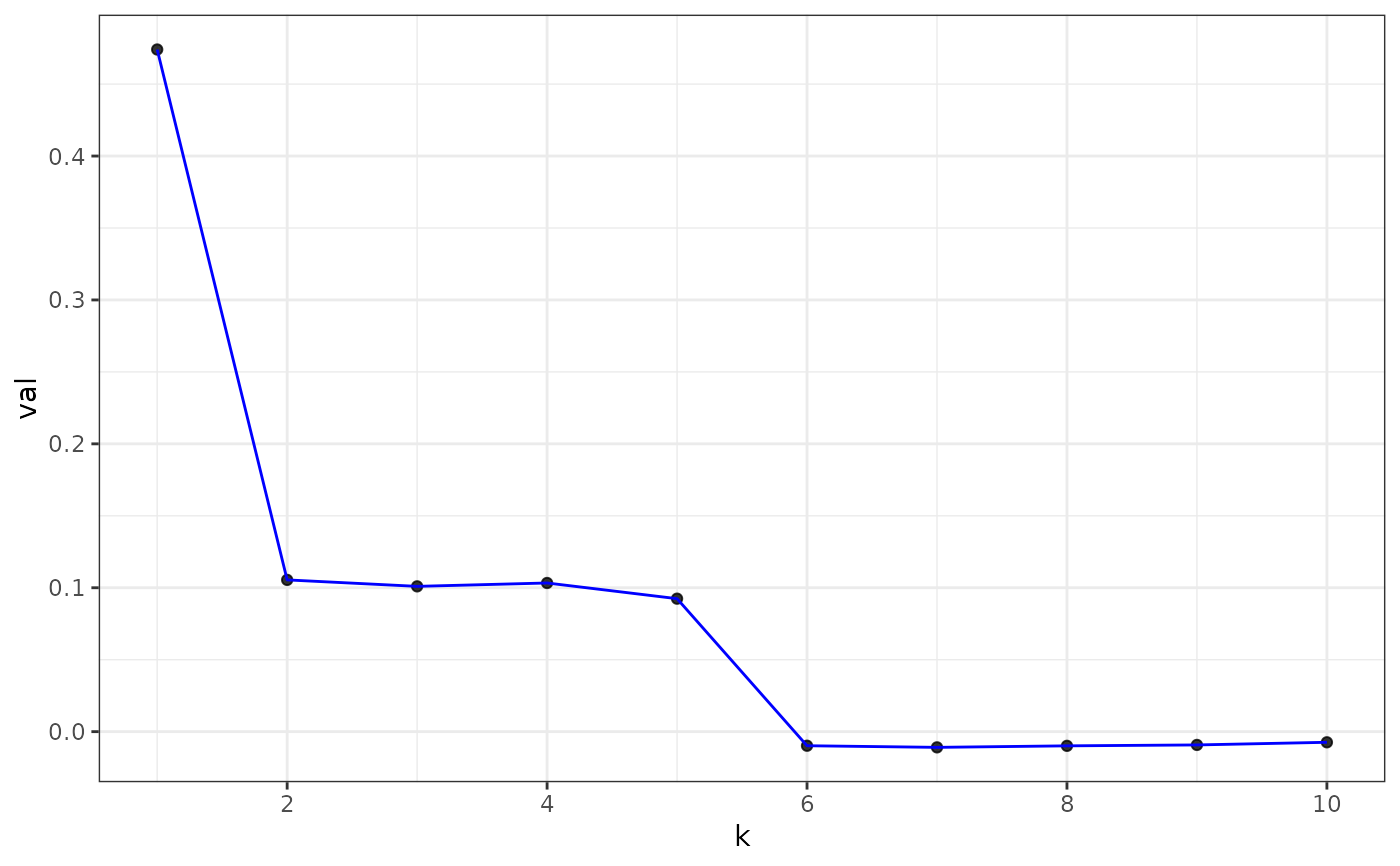
plot(eigs, type = "z-score")    # default

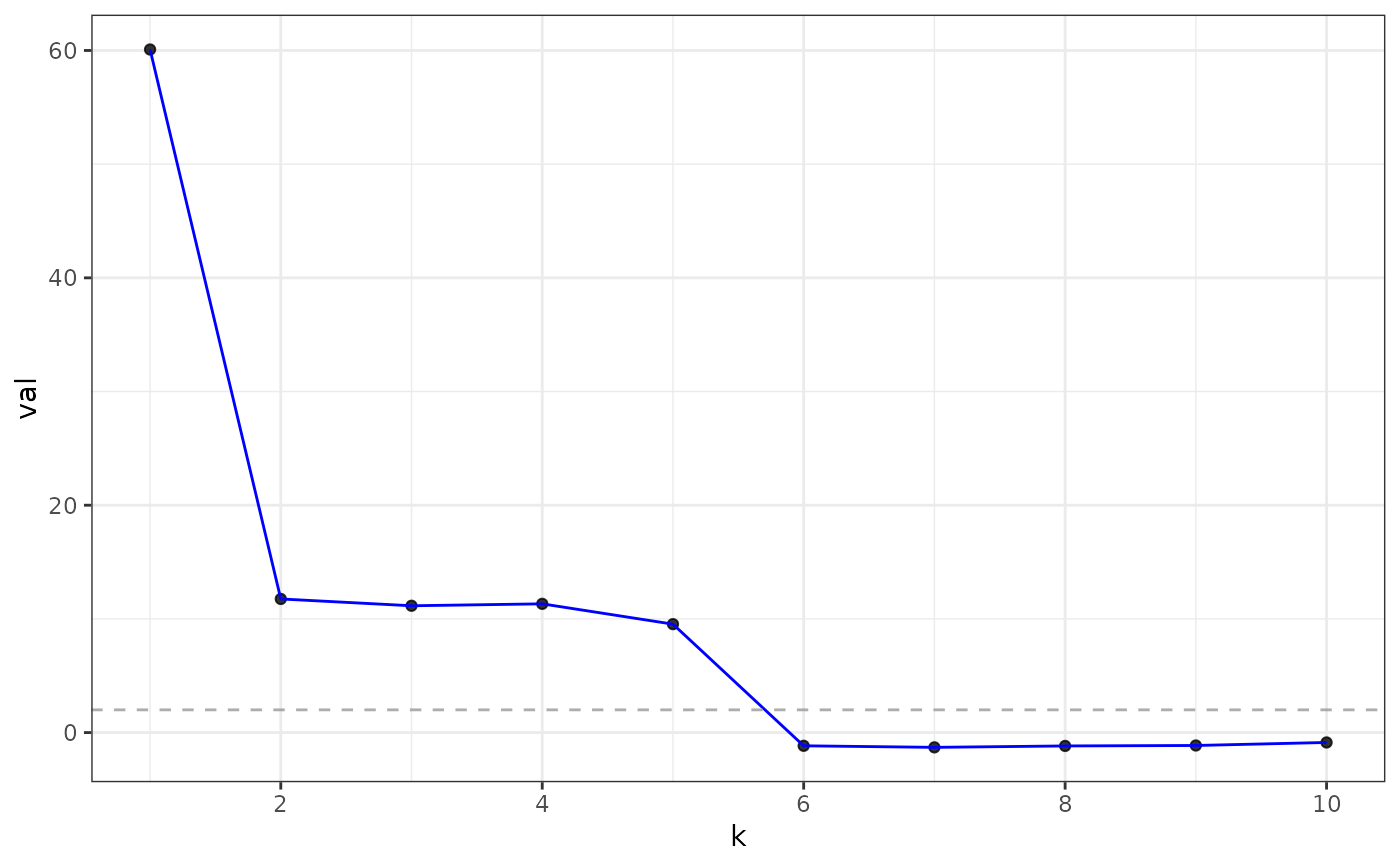plot(eigs, type = "adjacency")

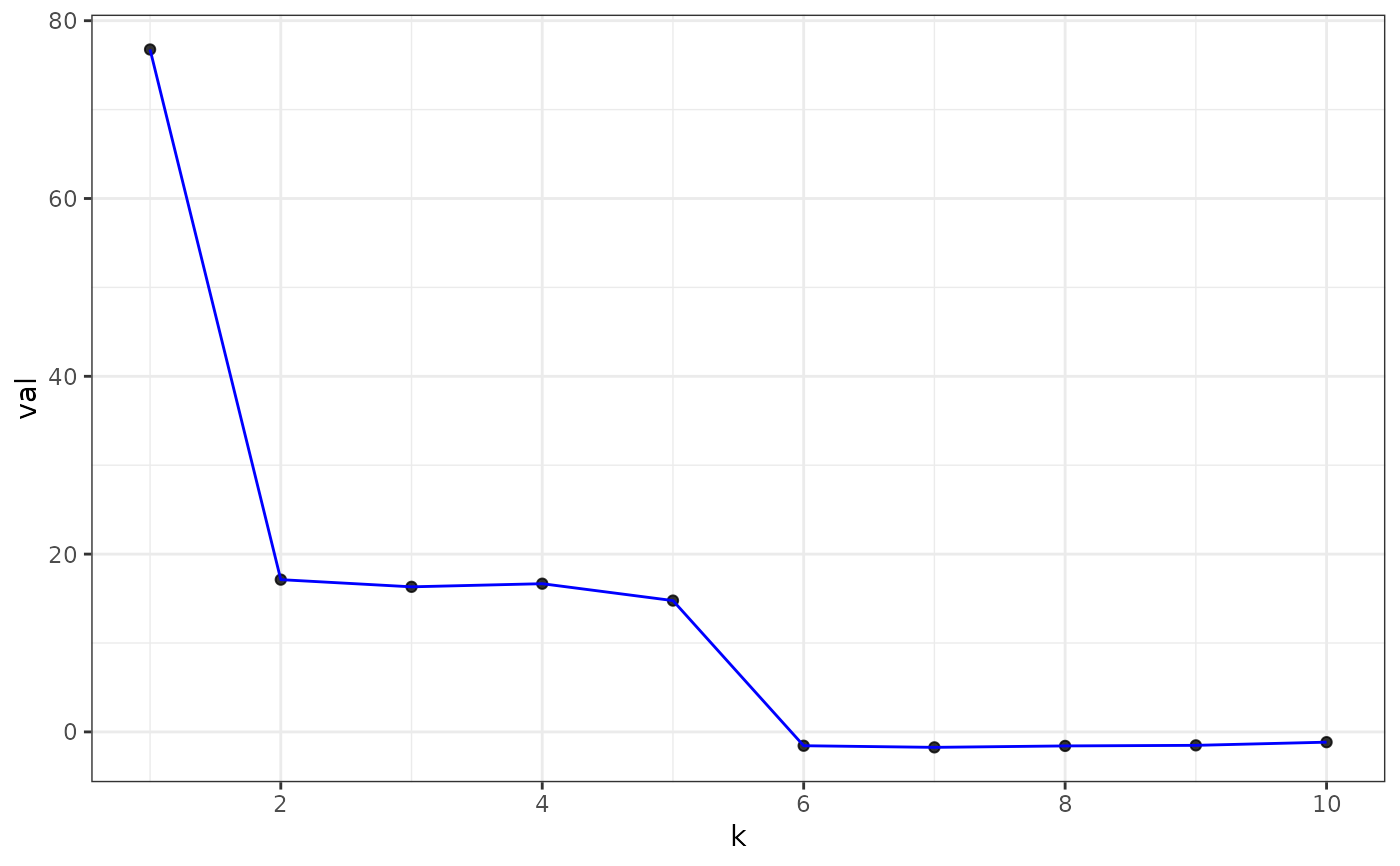plot(eigs, type = "laplacian")